C++算法之跟随滑动指针开疆拓土-编程社

1. 前言

双指针搜索算法，常见的有左右双指针；快慢双指针；先后双指针以及多指针……其中还包括一类滑动指针。

滑动指针也称为滑动窗口指针，其搜索实现即有灵性又透着优雅。

本文通过几个案例聊一聊滑动指针。

2. 最长的 1

题目描述

给定一个由若干 0 和 1 组成的数组 A，我们最多可以将 K 个值从 0 变成 1 。

返回包含最长（连续）1子数组的长度。如 A = [1,1,1,0,0,0,1,1,1,1,0], K = 2，则连续出现1的最长长度为6。

把最后一个0和倒数第二个0变成1，即[1,1,1,0,0,1,1,1,1,1,1]可得到最长连续1的长度。

算法实现流程：

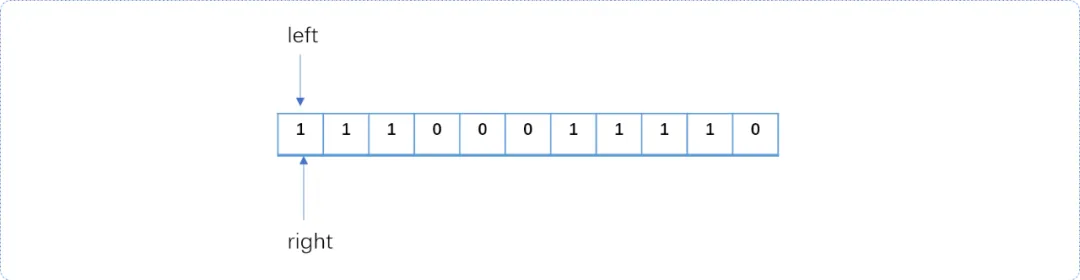
初始，left指针（左指针）指向最左边，right指针（右指针）和left指针同位置。相当于初始窗口紧闭状态。

right指针不停地向右边移动不间断地扩大窗口。移动条件是right指针指向的值为1，如果right指针所指向位置的值为0，则查询是否还有把0转换成1的机会，有则通过把0转换成1后移动。否则，right指针停止移动。
如下图所示，因k=2，可以将连续的两个0转换为1（红色表示0已经转换为1）。k的值在整个遍历过程中需要保留，可以另创建计数器变量c，计数已经使用过的0转换为1的次数。

当right指针停止移动后，意味着在原数列中找到了一段连续1的子序列。用变量res记录子序列的长度。Tips： 实际操作时，不需要真正把0变成1。

此时，right指针继续向前移动没有多大意义。需要等待左边释放用过的0转1的机会，方可以再次试探后面是否还有更多的连续1的子序列。让left指针向右边移动，直到遇到图中标记为红色的0（表示此处用过一次0转换为1的机会），让计数器c自减一，释放一次机会。则为右指针争取到了一次新的机会，把right位置的0变换为1,且继续向右边移动，直到再次遇到0。

Tips： 当left指针释放机会后，意味着原来的0变回了0，left指针需要多向前移一位。

根据上述描述，总结一下：

如果right指针所指向的值为1，则right指针向右边移动。
如果right指针指向的值为0，可以试着用掉0转1的机会。如果没有了机会，统计此时right和left之间1的个数。且right停止移动。
移动left指针直到遇到0，释放用过的机会。且left停止移动。
重复上述过程，直到right指针到达数组的末尾位置。

在left和right移动时，类似一扇窗窗户在从左向右滑动，把这种双指针称为滑动指针。

滑动指针的特点：

右指针移动过程中会扩大窗口范围，且移动过程会消费资源寻找解，本题的资源就是消耗0变成1的机会。
右指针在移动过程一旦消耗掉所有资源，就可以从左右指针所在范围内中获得一个解，此解不一定是最终解。
通过移动左指针释放资源，如回收0变成1的机会。
一旦释放资源后又继续让右指针移动，重复直到找到最终答案。

编码实现：

#include <bits/stdc++.h>
using namespace std;
int ones(int nums[],int len, int k) {
 int res=0,c=0;
 int left=0,right=0;
 while(right<len && left<len) {
  //right指针所指向的值为 1 或者还有机会
  while(nums[right]==1 || c<k  ) {
   //如果遇到0，则用掉机会
   if(nums[right]==0)c++;
   right++;
  }
  //当 right 停下来后,统计res
  res=max(res,right-left);
  //移动 left 释放机会
  while(  nums[left]!=0  ) left++;
  //释放机会
  c--;
  // 释放机会，意味着 1 又转换为 0，需要让 left 前进一位
  left++;
 }
 return res;
}
int main() {
 int nums[]= {1,0,1,0,0,0,1,1,0,1,0};
 int len=sizeof(nums)/4;
 int k=2;
 int res= ones(nums,len,k);
 cout<<res;
 return 0;
}

3、查找最短子串

问题描述：

现有字符串 S和字符串 T，请在字符串 S 里面找出包含T所有字母的最小子串。如果 ·S· 中不存这样的子串，则返回空字符串，如果 S 中存在这样的子串，需要保证有唯一的答案。

如输入 S="ADOBECODEBANC"，T="ABC"。则输出："BANC"。

算法分析：

此题中，可以把T当成资源，一边扫描S一边查找是否存在T中的字符，有则消耗掉，直到消耗掉T中的所有资源。得到一个解后再移动左指针，释放资源。重复这个过程。

下面使用图示演示整个过程。

初始状态。左指针和右指针指向同一个位置。

右指针向右边移动，直到包含完字符串T中的所有字符。

移动左指针释放窗口中的资源字符前，计算此时左右指针之间的距离，即一个有效解，但不是最终解。直到左右窗口中没有完整的T字符串时激活右指针移动。

左指针向右边移动，一边收窄窗口释放资源，一边统计此时左右之间的距离。

总结一下：

右指针向右移动直到左右指针所在窗口中包含完整的T字符串资源。
左指针每移动一步后，只要左右窗口中的包含完整的T资源就计算当前的左右指针的距离，直到左右指针中不再包含完整的T资源。
当右指针指向数列最末尾时，整个算法结束。

算法实现：算法实现过程中，需要如下几个信息。

算法中需要记录实际所需要的资源信息。
在扩展窗口时，统计被包含的资源信息以及记录是否已经完全包含。

#include <bits/stdc++.h>
using namespace std;

string getShort(string str,string t) {
 int size=str.size();
 //左右指针初始位置
 int left=0,right=0;
 //记录资源信息
 int sources[26]= {0};
 //记录窗口中已经使用的资源
 int wins[26]= {0};
 //计数器
 int count=0;
 //实际有效资源的数量
 int scount=0;
 //记录最终位置和结束位置
 int sta=0,end=size;
 //把字符串数字化，便于比较
 for(int i=0; i<t.size(); i++) {
  //简化问题，假设字符串全部为大写
  sources[ t[i]-'A' ]++;
  scount++;
 }
 while( right<size ) {
  char c=str[right];
  //检查是不是资源
  if( sources[c-'A']!=0 ) {
   //记录在窗口中
   wins[c-'A']++;
   //如果某个字符全部在窗口中
   if(wins[c-'A']==sources[c-'A'])count++;
  }
  right++;
  while( count==scount  ) {
   //如果窗口中已经包含所有资源，则移动左窗口，移动之前计算此时左右指针的距离
   if(right-left<end-sta)
    sta=left,end=right;
   //移动左指针之前记录移出的字符
   char mc=str[left];
   //移动左指针
   left++;
   //检查移出去的字符是不是资源
   if( sources[mc-'A']!=0 ) {
    //从窗口信息表中移走
    wins[mc-'A']--;
                 //某个字符全部释放
    if( wins[mc-'A']==0)count--;
   }
  }
 }
 return end-sta==size?"-1":str.substr(sta,end-sta);
}
int main() {
 string res= getShort("AAOBC","ABC");
 cout<<res;
 return 0;
}

4、异位词

问题描述： 给定一个字符串s和一个非空字符串p，找到s中所有是p的字母异位词的子串，返回这些子串的起始索引。字符串只包含小写英文字母，并且字符串s和p的长度都不超过20100。

说明：字母异位词指字母相同，但排列不同的字符串。不考虑答案输出的顺序。示例 1：输入：s："cbaebabacd" p："abc"。输出：[0，6]。解释：起始索引等于0的子串是"cba"它是"abc"的字母异位词。起始索引等于6的子串是"bac"，它是"abc”的字母异位词。

此题和上题的题意差不多。区别在于，左右指针所限制的窗口中除了要包含资源之外，还需要有长度限制，就是在窗口只能包含资源中的所有字符。

算法实现：

#include <bits/stdc++.h>
using namespace std;

vector<int> getShort(string str,string t) {
 int size=str.size();
 //左右指针初始位置
 int left=0,right=0;
 //记录资源信息
 int sources[26]= {0};
 //记录窗口中已经使用的资源
 int wins[26]= {0};
 //计数器
 int count=0;
 //实际有效资源的数量
 int scount=0;
 //记录位置
 vector<int> res;
 //把字符串数字化，便于比较
 for(int i=0; i<t.size(); i++) {
  //简化问题，假设字符串全部为大写
  sources[ t[i]-'a' ]++;
  scount++;
 }
 while( right<size ) {
  char c=str[right];
  //检查是不是资源
  if( sources[c-'a']!=0 ) {
   //记录在窗口中
   wins[c-'a']++;
   //如果某个字符全部在窗口中
   if(wins[c-'a']==sources[c-'a'])count++;
  }
  right++;
  while( count==scount  ) {
   //如果窗口中已经包含所有资源，则移动左窗口，移动之前计算此时左右指针的距离
   if(right-left==t.size())
                 //如果左右指针所包含的窗口的长度恰好等于资源字符串的长度，则存储存其位置
    res.push_back(left);
   //移动左指针之前记录移出的字符
   char mc=str[left];
   //移动左指针
   left++;
   //检查移出去的字符是不是资源
   if( sources[mc-'a']!=0 ) {
    //从窗口信息表中移走
    wins[mc-'a']--;
    if( wins[mc-'a']==0)count--;
   }
  }
 }
 return res;
}
//测试
int main() {
 vector<int> res= getShort("cbaebabacd","abc");
 for(int i=0;i<res.size();i++)cout<<res[i]<<"\t";
 return 0;
}